21. Streaming algorithm for the mean () and the variance (2) (Knuth, Welford). Show with an example why the running mean formula is preferable to the definition formula.
in the previous post, we saw what mean is and now we will introduce a new term variance or standard deviation. The standard deviation is a measure of how much a dataset differs from its mean; it tells us how dispersed the data are. A dataset that’s pretty much clumped around a single point would have a small standard deviation, while a dataset that’s all over the map would have a large standard deviation.
Given a sample x1,…,xN , the standard deviation is defined as the square root of the variance:
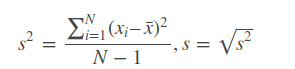The definition can be converted directly into an algorithm that computes the variance and standard deviation in two passes: compute the mean in one pass over the data, and then do a second pass to compute the squared differences from the mean. Doing two passes is not ideal though, and it can be impractical in some settings. For example, if the samples are generated by a random simulation it may be prohibitively expensive to store samples just so you can do a second pass over them.
This is one of those cases where a mathematically simple approach turns out to give wrong results for being numerically unstable. In simple cases the algorithm will seem to work fine, but eventually you will find a dataset that exposes the problem with the algorithm. If the variance is small compared to the square of the mean, and computing the difference leads catastrophic cancellation where significant leading digits are eliminated and the result has a large relative error. In fact, you may even compute a negative variance, which is mathematically impossible.
Welford’s method is a usable single-pass method for computing the variance. It can be derived by looking at the differences between the sums of squared differences for N and N-1 samples. It’s really surprising how simple the difference turns out to be:
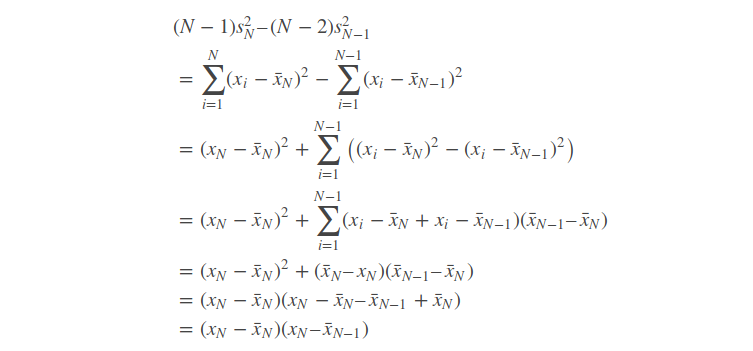
This means we can compute the variance in a single pass using the following algorithm:
Welford’s method, which gives us accurate estimates of mean and variance without having to keep a bunch of data in memory. The advantage of Welford’s method is that it requires only one pass. Forexample, I generated each sample, updated Welford’s variables, and threw the sample away. But to use the direct method, I had to store the 1,000,000 random samples before computing the variance.