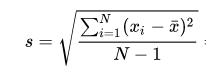22b. The concept of dispersion and the most “popular” statistics to quantify it.
In statistics, dispersion (also called variability, scatter, or spread) is the extent to which a distribution is stretched or squeezed. Dispersion is contrasted with location or central tendency, and together they are the most used properties of distributions. Dispersion in statistics is a way of describing how spread out a set of data is. When a data set has a large value, the values in the set are widely scattered; when it is small the items in the set are tightly clustered. Very basically,
this set of data has a small value: 1, 2, 2, 3, 3, 4
…and this set has a wider one: 0, 1, 20, 30, 40, 100
Common examples of measures of statistical dispersion are the variance, standard deviation, and interquartile range.
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its mean. Informally, it measures how far a set of (random) numbers are spread out from their average value. Variance has a central role in statistics, where some ideas that use it include descriptive statistics, statistical inference, hypothesis testing, goodness of fit, and Monte Carlo sampling. Variance is an important tool in the sciences, where statistical analysis of data is common. The variance is the square of the standard deviation, the second central moment of a distribution, and the covariance of the random variable with itself.
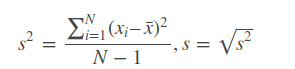
Standard deviation is a measure of dispersement in statistics. “Dispersement” tells you how much your data is spread out. Specifically, it shows you how much your data is spread out around the mean or average. For example, are all your scores close to the average? Or are lots of scores way above (or way below) the average score?